排序算法小结

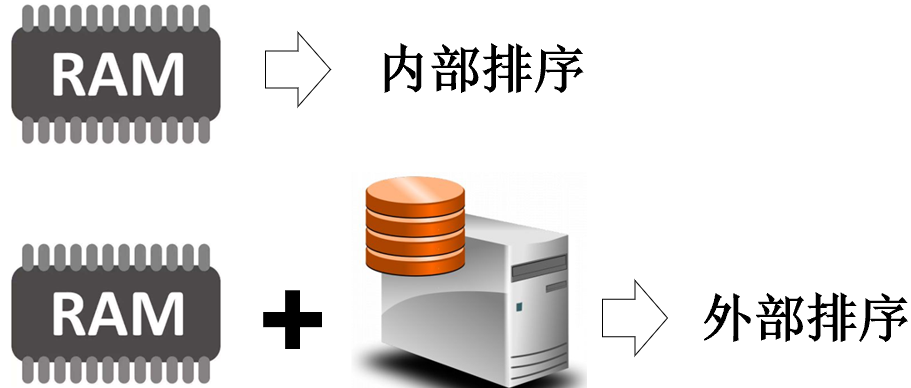
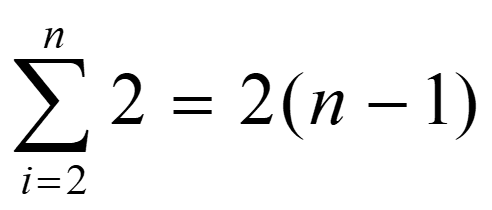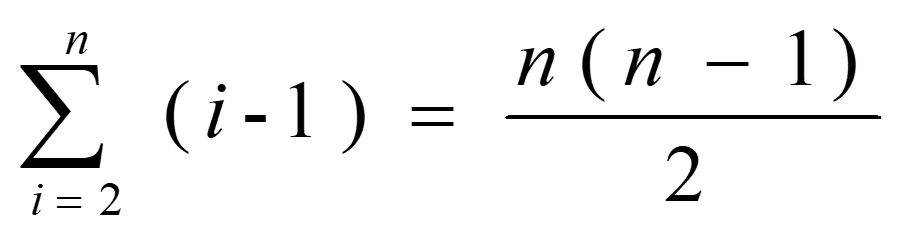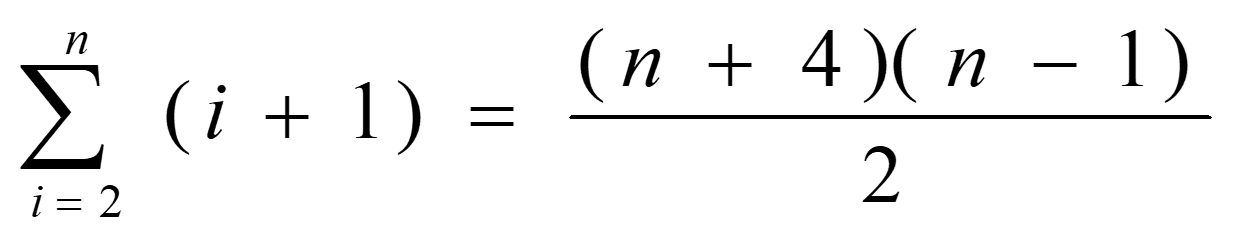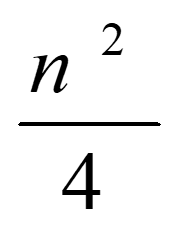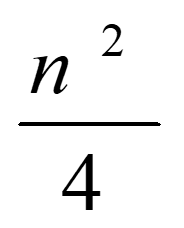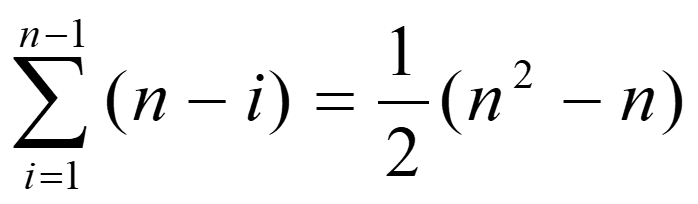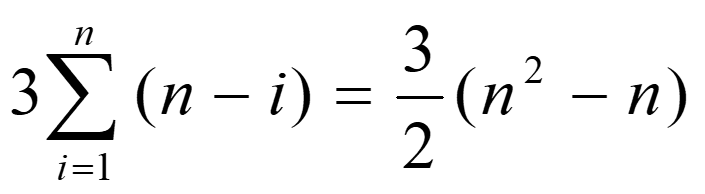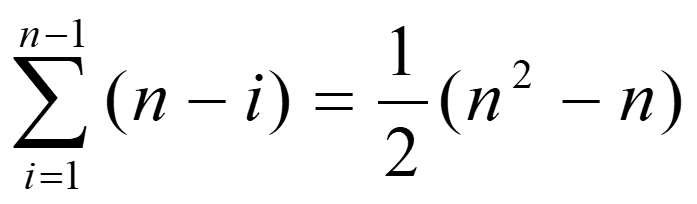内部排序与外部排序

内部排序是指在内存中进行的排序，数据量较小，可以一次性全部读入内存进行排序。 而外部排序是指数据量较大，无法一次性全部读入内存，需要将数据分成若干个小块，每次读入一部分数据进行排序，最后将排好序的小块合并成一个有序的大块。排序算法往往指的是内部排序算法，即数据记录在内存中进行排序。内部排序的过程是一个逐步扩大记录的有序序列长度的过程。

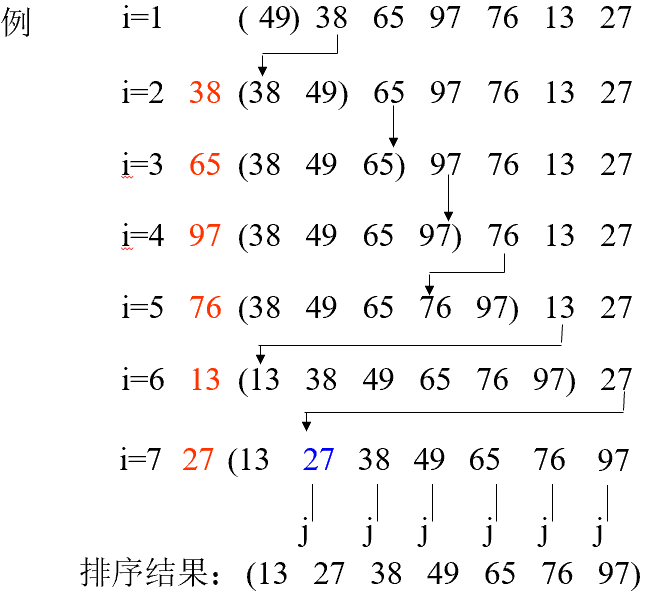
插入排序

直接插入

•排序过程：先将序列中第1个记录看成是一个有序子序列，然后从第2个记录开始，逐个进行插入，直至整个序列有序。整个排序过程为n-1趟插入。

•算法描述

typedef struct
{  int key;
   float info;
}JD;

void straisort(JD r[],int n)//对长度为n的序列排序
{  int i,j;
   for(i=2;i<=n;i++)
   {  r[0]=r[i];
      j=i-1;
      while(r[0].key<r[j].key)
      {  r[j+1]=r[j];
         j--;
      }
      r[j+1]=r[0];
   }
} 

•算法评价

-时间复杂度: $T(n)=O(n^2)$

»若待排序记录按关键字从小到大排列(正序)

关键字比较次数：

记录移动次数：

»若待排序记录按关键字从大到小排列(逆序)

关键字比较次数：

记录移动次数：

»若待排序记录是随机的，取平均值

关键字比较次数：

记录移动次数：

-空间复杂度：$S(n)=O(1)$

二分插入

也叫折半插入排序

•排序过程：用折半查找方法确定插入位置的排序

•算法描述

void binsort(JD r[],int n)//折半插入排序
{  int i,j,x,s,m,k;
   for(i=2;i<=n;i++)
   {  r[0]=r[i];
      x=r[i].key;
      s=1; j=i-1;
      while(s<=j)//查找插入位置
      {  m=(s+j)/2;
         if(x<r[m].key)  j=m-1;
         else s=m+1;
      }
      for(k=i-1;k>=s;k--)//移动
         r[k+1]=r[k];
      r[s]=r[0];//插入
   }
}

•算法评价

-时间复杂度：$T(n)=O(n^2)$

-空间复杂度：$S(n)=O(1)$

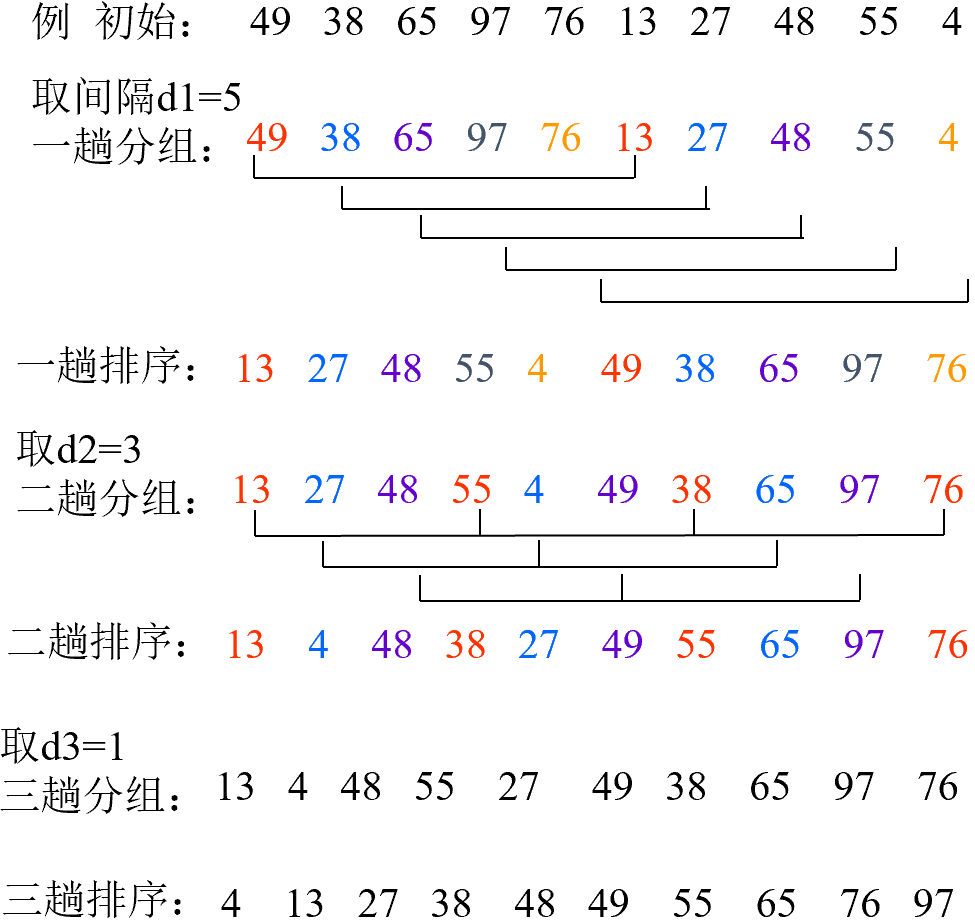
希尔排序

又称缩小增量法

•排序过程：用折半查找方法确定插入位置的排序

•算法描述

void shellsort(JD r[],int n,int d[T]) // d[T]是已经初始化的间隔数组
{  int i,j,k;
   JD x;
   k=0;
   while(k<T) 
   {  for(i=d[k]+1;i<=n;i++)
      {  x=r[i]; //r[i]是第k次分组的某个分组的某个元素， 用x暂存
         j=i-d[k]; 
         while((j>0)&&(x.key<r[j].key))  //将这个分组中，大于x的关键字后移
         {  r[j+d[k]]=r[j];
            j=j-d[k];
         }
         r[j+d[k]]=x; //将x插入到这个分组的合适位置
       }
       k++;
    }
}

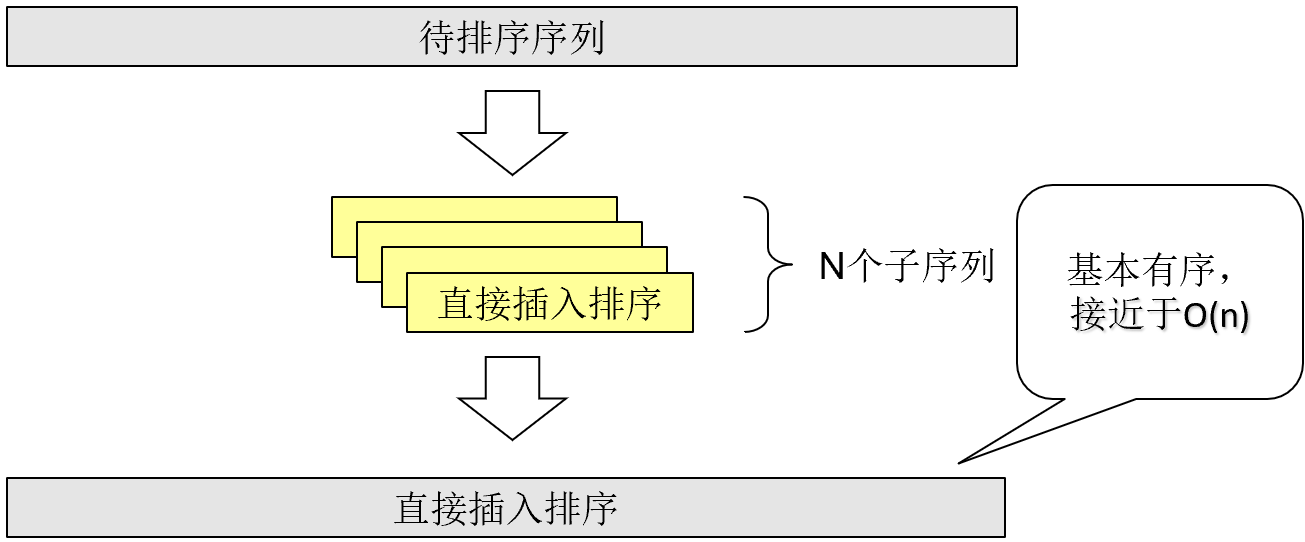
•希尔排序特点

交换排序

冒泡排序

•排序过程

改进：上一趟排序记录最后一次交换的位置，作为下一趟排序的结束位置。

•算法描述

void BubbleSort(Elem R[ ], int n) {
  i = n;
  while (i >1) {
     lastExchangeIndex = 1;
     for (j = 1;  j < i;  j++)
     if (R[j].key > R[j+1].key) {  
         Swap(R[j], R[j+1]);
         lastExchangeIndex = j;  /*记下进行交换的记录位置*/
     } 
     i = lastExchangeIndex; /*本趟最后一次交换的位置*/
  } 
} 

•算法评价

-时间复杂度：$T(n)=O(n^2)$

»最好情况（正序）

比较次数：n-1

移动次数：0

»最坏情况（逆序）

比较次数：

移动次数：

-空间复杂度：$S(n)=O(1)$

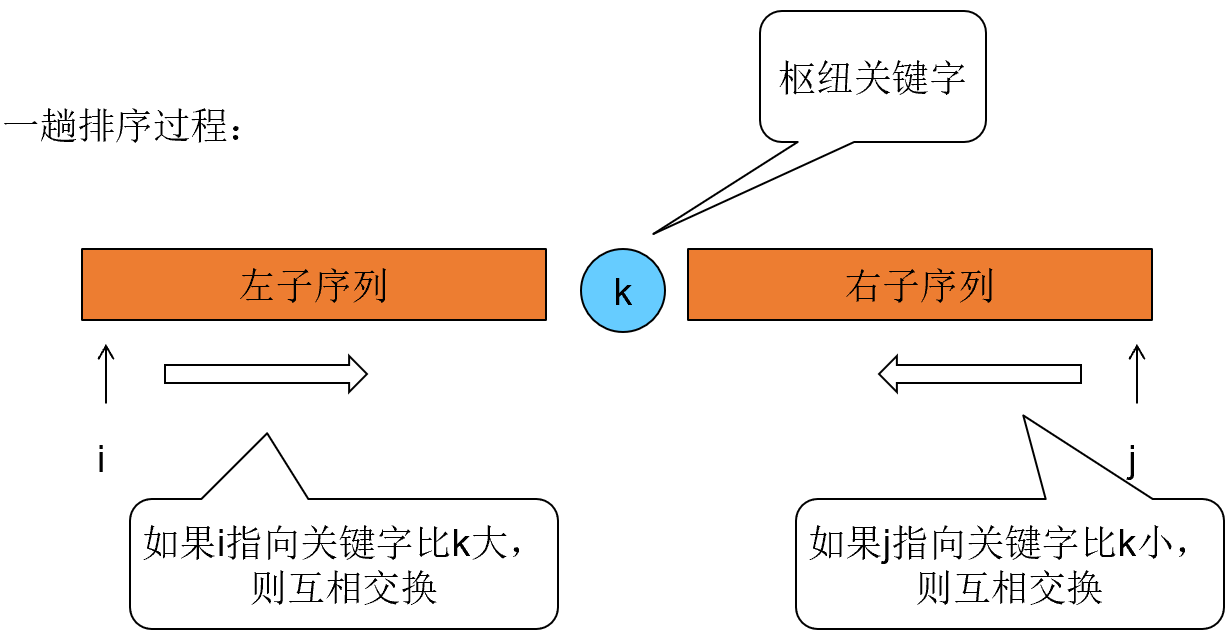
快速排序

•排序过程

•算法描述

void qksort(JD r[],int t,int w)//t=low,w=high
{  int i,j,k;
   JD x;
   if(t>=w)  return;
   i=t; j=w; x=r[i];
   while(i<j)
   {  while((i<j)&&(r[j].key>=x.key))  j--;//枢轴后面的值大于枢轴
      if(i<j) { r[i]=r[j]; i++; }//当不满足时，与枢轴交换
      while((i<j)&&(r[i].key<=x.key))  i++;//枢轴前面的值小于枢轴
      if(i<j) { r[j]=r[i]; j--; }//不满足，与枢轴交换
   }
   r[i]=x;
   qksort(r,t,j-1);
   qksort(r,j+1,w);
}

•算法评价

-时间复杂度：$T(n)=O(n^2)$

»最好情况（每次总是选到中间值作划分元）$T(n)=O(nlog_2n)$

»最坏情况（每次总是选到最小或最大元素作划分元）$T(n)=O(n^2)$

-空间复杂度：需栈空间以实现递归

»最坏情况：$S(n)=O(n)$

»一般情况：$S(n)=O(log_2n)$

常用“三者取中”法来选取划分记录，即取首记录r[s].key.尾记录r[t].key和中间记录r[(s+t)/2].key三者的中间值为划分记录。

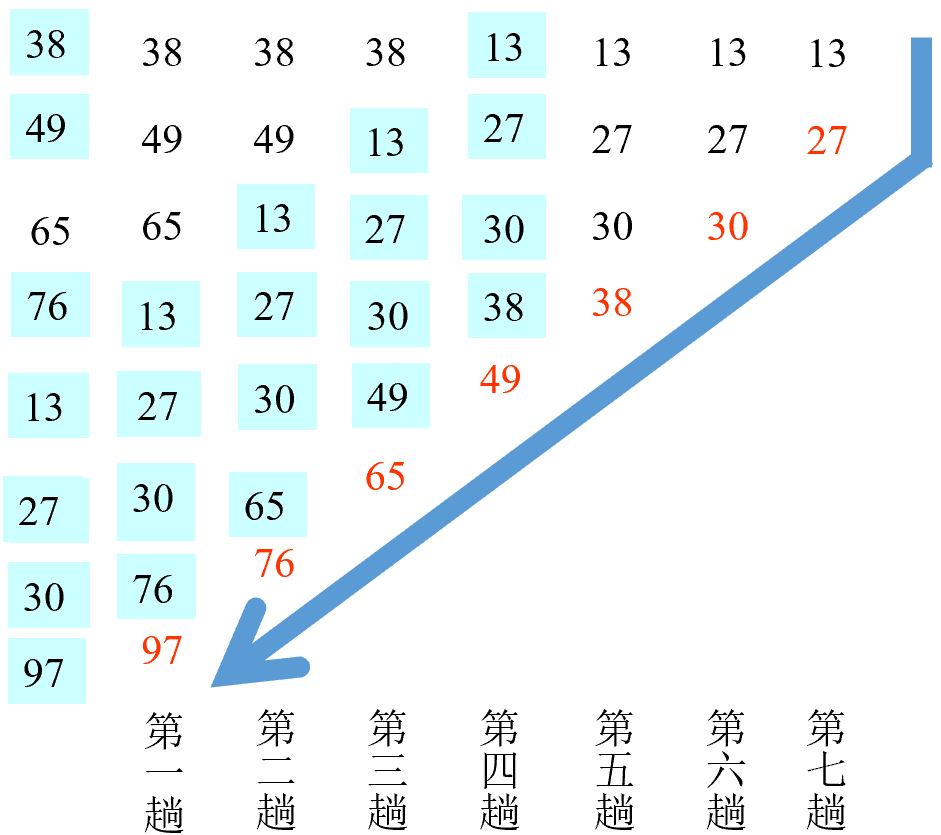
选择排序

简单选择排序

•排序过程

1. 首先通过n-1次关键字比较，从n个记录中找出关键字最小的记录，将它与第一个记录交换

2. 再通过n-2次比较，从剩余的n-1个记录中找出关键字次小的记录，将它与第二个记录交换

3. 重复上述操作，共进行n-1趟排序后，排序结束

•算法描述

void smp_selesort(JD r[],int n)
{  int i,j,k;
   JD x;
   for(i=1;i<n;i++)
   {  k=i;
      for(j=i+1;j<=n;j++)
         if(r[j].key<r[k].key)  k=j;
      if(i!=k)
      {  x=r[i];
         r[i]=r[k];
         r[k]=x;
      }
   }
}

•算法评价

-时间复杂度: $T(n)=O(n^2)$

»记录移动次数

Y最好情况：0

Y最坏情况：3(n-1)

»比较次数：

-空间复杂度：$S(n)=O(1)$

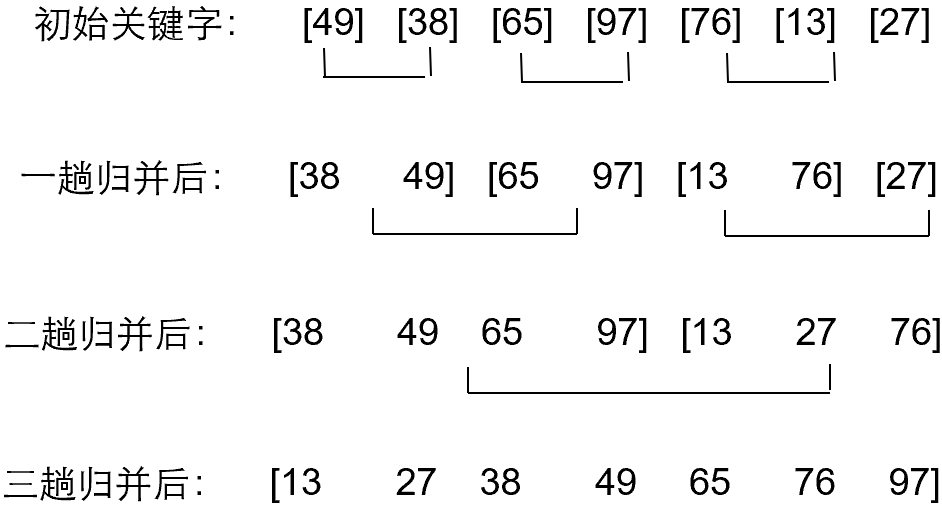
归并排序

2-路归并排序

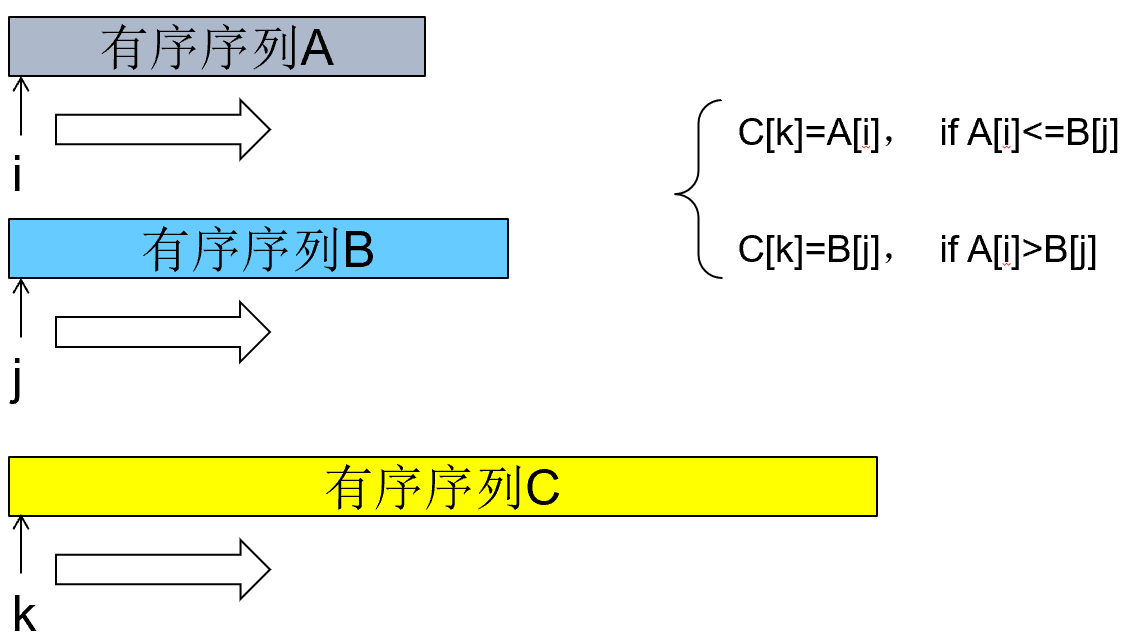
•排序过程

1. 设初始序列含有n个记录，则可看成n个有序的子序列，每个子序列长度为1
2. 两两合并，得到$n/2$下取整个长度为2或1的有序子序列
3. 再两两合并，……如此重复，直至得到一个长度为n的有序序列为止

•算法描述

void merge(int SR[], int first,int mid, int last, int TR[])  
{ 
   int i,j,k; 
   i=first; j=mid+1;k=1;
   while ((i <= mid) && (j <= last)){
         if （SR[i]>SR[j]）{TR[k]=SR[j]; 
             j=j+1; 
             k=k+1;}
          else
             {TR[k]=SR[i]};
               i=i+1;
               k=k+1;}
    }
    while (i<=mid){
       TR[k]=SR[i]; i=i+1; k=k+1;}
    while (j<=last){
       TR[k]=SR[j]; j=j+1; k=k+1;}
}  

void mergesort(int SR[], int first, int last, int TR[])  
{  
    int temp[]; // temp分两段存储左边和右边的子序列
    if (first < last)  
    {  
        mid = (first + last) / 2;  
        mergesort(SR, first, mid, temp);    //左边有序  
        mergesort(SR, mid + 1, last, temp); //右边有序  
        merge(temp, first, mid, last, TR); //再将二个有序数列合并  
    }  
   else
   {
       TR[first] = SR[first];
   }
}  

•算法评价

-时间复杂度：每一趟归并的时间复杂度为$O(n)$， 总共需要归并$log2n$趟，因而，总的时间复杂度为$O(nlog2n)$。

-空间复杂度：2-路归并排序过程中，需要一个与表等长的存储单元数组空间，因此，空间复杂度为$O(n)$。

排序方法比较

排序方法选择主要考虑

• 待排序记录的数量
• 关键字的分布情况
• 对排序稳定性要求

时间特性

时间复杂度为$O(nlogn)$:快速、归并排序

时间复杂度为$O(n^2)$:插入、冒泡、选择排序，插入最常用，尤其基本有序时，选择记录移动次数最少

当待排序记录基本有序时：插入和冒泡可达到$O(n)$ ；

选择、归并排序的时间特性不随关键字分布而改变

对照表

排序方法	平均时间	最坏情况	最好情况	辅助空间	稳定性
直接插入排序（含二分）	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	√
希尔排序	很复杂，是增量d的函数	很复杂	很复杂	$O(1)$	×
选择排序	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	×
冒泡排序	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	√
快速排序	$O(nlogn)$	$O(n^2)$	$O(nlogn)$	$O(logn)$	×
归并排序	$O(nlogn)$	$O(nlogn)$	$O(nlogn)$	$O(n)$	√