问题描述

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

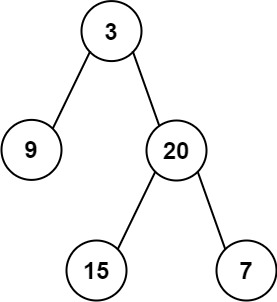
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

  • 节点数在 [1, 1000] 范围内
  • -1000 <= Node.val <= 1000

核心思路

一个节点为「左叶子」节点，当且仅当它是某个节点的左子节点，并且它是一个叶子结点。因此我们可以考虑对整棵树进行遍历，当我们遍历到节点 node 时，如果它的左子节点是一个叶子结点，那么就将它的左子节点的值累加计入答案。

code

深度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool isLeafNode(TreeNode* node) {
        return !node->left && !node->right;
    }

    int dfs(TreeNode* node) {
        int ans = 0;
        if (node->left) {
            ans += isLeafNode(node->left) ? node->left->val : dfs(node->left);
        }
        if (node->right && !isLeafNode(node->right)) {
            ans += dfs(node->right);
        }
        return ans;
    }

    int sumOfLeftLeaves(TreeNode* root) {
        return root ? dfs(root) : 0;
    }
};

  • 时间复杂度：O(n)O(n)，其中 n 是树中的节点个数。

  • 空间复杂度：O(n)O(n)。空间复杂度与深度优先搜索使用的栈的最大深度相关。在最坏的情况下，树呈现链式结构，深度为 O(n)O(n)，对应的空间复杂度也为 O(n)O(n)。

广度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    bool isLeafNode(TreeNode* node) {
        return !node->left && !node->right;
    }

    int sumOfLeftLeaves(TreeNode* root) {
        if (!root) {
            return 0;
        }

        queue<TreeNode*> q;
        q.push(root);
        int ans = 0;
        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();
            if (node->left) {
                if (isLeafNode(node->left)) {
                    ans += node->left->val;
                }
                else {
                    q.push(node->left);
                }
            }
            if (node->right) {
                if (!isLeafNode(node->right)) {
                    q.push(node->right);
                }
            }
        }
        return ans;
    }
};

  • 时间复杂度：O(n)O(n)，其中 n 是树中的节点个数。

  • 空间复杂度：O(n)O(n)。空间复杂度与广度优先搜索使用的队列需要的容量相关，为 O(n)O(n)。