leetcode 700.二叉搜索树中的搜索

问题描述

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

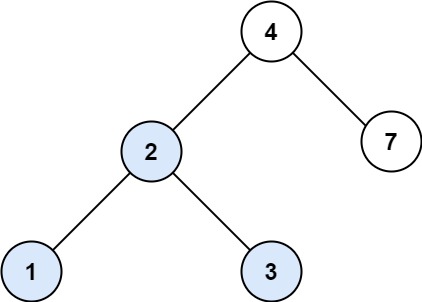
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

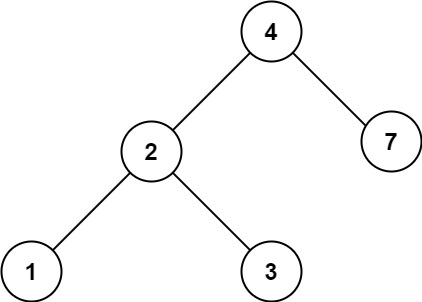
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

树中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107

递归

核心思路

二叉搜索树满足如下性质：

左子树所有节点的元素值均小于根的元素值；
右子树所有节点的元素值均大于根的元素值。

据此可以得到如下算法：

若 $\textit{root}$ 为空则返回空节点；
若 $\textit{val}=\textit{root}.\textit{val}$ ，则返回 $\textit{root}$ ；
若 $\textit{val}<\textit{root}.\textit{val}$ ，递归左子树；
若 $\textit{val}>\textit{root}.\textit{val}$ ，递归右子树。

code

class Solution {
public:
    TreeNode *searchBST(TreeNode *root, int val) {
        if (root == nullptr) {
            return nullptr;
        }
        if (val == root->val) {
            return root;
        }
        return searchBST(val < root->val ? root->left : root->right, val);
    }
};

时间复杂度： $O(N)$ ，其中 N 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链，且要找的元素比链末尾的元素值还要小（大），这种情况下我们需要递归 N 次。
空间复杂度： $O(N)$ 。最坏情况下递归需要 $O(N)$ 的栈空间。

迭代

核心思路

递归改成迭代写法：

若 $\textit{root}$ 为空则跳出循环，并返回空节点；
若 $\textit{val}=\textit{root}.\textit{val}$ ，则返回 $\textit{root}$ ；
若 $\textit{val}<\textit{root}.\textit{val}$ ，将 $\textit{root}$ 置为 $\textit{root}.\textit{left}$ ；
若 $\textit{val}>\textit{root}.\textit{val}$ ，将 $\textit{root}$ 置为 $\textit{root}.\textit{right}$ 。

code

class Solution {
public:
    TreeNode *searchBST(TreeNode *root, int val) {
        while (root) {
            if (val == root->val) {
                return root;
            }
            root = val < root->val ? root->left : root->right;
        }
        return nullptr;
    }
};