leetcode 701.二叉搜索树中的插入操作

问题描述

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果 。

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

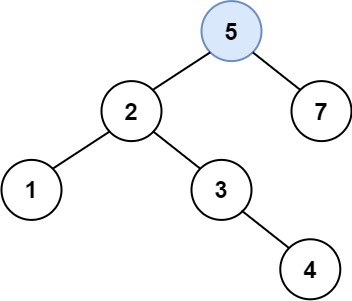
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。

核心思路

插入和搜索操作其实差不多。

当将 $\textit{val}$ 插入到以 $\textit{root}$ 为根的子树上时，根据 $\textit{val}$ 与 $\textit{root.val}$ 的大小关系，就可以确定要将 $\textit{val}$ 插入到哪个子树中。

如果该子树不为空，则问题转化成了将 $\textit{val}$ 插入到对应子树上。
否则，在此处新建一个以 $\textit{val}$ 为值的节点，并链接到其父节点 $\textit{root}$ 上。

code

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr) {
            return new TreeNode(val);
        }
        TreeNode* pos = root;
        while (pos != nullptr) {
            if (val < pos->val) {
                if (pos->left == nullptr) {
                    pos->left = new TreeNode(val);
                    break;
                } else {
                    pos = pos->left;
                }
            } else {
                if (pos->right == nullptr) {
                    pos->right = new TreeNode(val);
                    break;
                } else {
                    pos = pos->right;
                }
            }
        }
        return root;
    }
};