问题描述

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

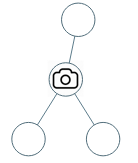
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

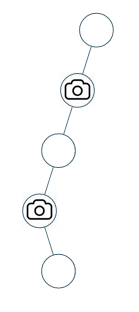
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

  1. 给定树的节点数的范围是 [1, 1000]。
  2. 每个节点的值都是 0。

核心思路

核心思路

局部最优：让叶子节点的父节点安摄像头，所用摄像头最少。

整体最优：全部摄像头数量所用最少。

从下到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

实现要点

  1. 二叉树的遍历

    使用后序遍历也就是左右中的顺序，在回溯的过程中从下到上进行推导。

  2. 如何隔两个节点放一个摄像头

    每个节点可能有如下三种状态，空节点的状态只能是有覆盖，才能在叶子节点的父节点放摄像头：

    • 0：该节点无覆盖
    • 1：本节点有摄像头
    • 2：本节点有覆盖

    单层逻辑处理有如下四类情况：

    • 情况1：左右节点都有覆盖

    中间节点应该是无覆盖的状态。

    • 情况2：左右节点至少有一个无覆盖的情况

    摄像头数量+1，并且return 1，代表中间节点放摄像头。

    • 情况3：左右节点至少有一个有摄像头

    其父节点就应该是2（覆盖的状态）。

    • 情况4：头结点没有覆盖

      递归结束之后，还要判断根节点，如果没有覆盖，result++。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {

        // 空节点，该节点有覆盖
        if (cur == NULL) return 2;

        int left = traversal(cur->left);    // 左
        int right = traversal(cur->right);  // 右

        // 情况1
        // 左右节点都有覆盖
        if (left == 2 && right == 2) return 0;

        // 情况2
        // left == 0 && right == 0 左右节点无覆盖
        // left == 1 && right == 0 左节点有摄像头，右节点无覆盖
        // left == 0 && right == 1 左节点有无覆盖，右节点摄像头
        // left == 0 && right == 2 左节点无覆盖，右节点覆盖
        // left == 2 && right == 0 左节点覆盖，右节点无覆盖
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }

        // 情况3
        // left == 1 && right == 2 左节点有摄像头，右节点有覆盖
        // left == 2 && right == 1 左节点有覆盖，右节点有摄像头
        // left == 1 && right == 1 左右节点都有摄像头
        // 其他情况前段代码均已覆盖
        if (left == 1 || right == 1) return 2;

        // 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解
        // 这个 return -1 逻辑不会走到这里。
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // 情况4
        if (traversal(root) == 0) { // root 无覆盖
            result++;
        }
        return result;
    }
};

  • 时间复杂度: O(n)O(n)，需要遍历二叉树上的每个节点。

  • 空间复杂度: O(n)O(n)